-
N - Slimes / atcoder.jpatcoder.jp 2020. 1. 21. 10:58728x90
문제링크 : https://atcoder.jp/contests/dp/tasks/dp_n
문제해설 : https://jinpyo.kim/EducationalDP-solution
Submission : https://atcoder.jp/contests/dp/submissions/9653540
Java source : https://github.com/skysign/WSAPT/blob/master/atcoder.jp/N%20-%20Slimes/src/Main.java여러개의 슬라임을 2개씩 합칠 때, 합치는 비용을 고려해서, 가장 적은 비용으로 합치는 방법을 찾는 문제입니다.
이 문제를 DP가 방식이 아니라, 아주 간단하게 생각해서, 인접한 두수의 합이 최소가 되는 방식으로, 2개의 슬라임을 합처나가면, 최소비용으로 합칠 수 있지 않을까? 라고 생각할 수도 있습니다. 문제에서 주어진 Sample Input은 그 방식으로 풀어도 답이 나오지만, 아래의 샘플 인풋은 그 방식으로 풀 수 없습니다. 이 문제는 DP로 풀어야만 합니다.
4 40 30 30 50(40, 30, 30, 50) → (40, 60, 50) : 60
(40, 60, 50) → (100, 50) : 100
(100, 50) → (150) : 150
60 + 100 + 150 = 310
그 방식으로 풀면, 310 이 합치는 비용입니다.DP 방식으로 풀면, 300 이 합치는 비용입니다.
(40, 30, 30, 50) → (70, 30, 50) : 70
(70, 30, 50) → (70, 80) : 80
(70, 80) → (150) : 150
70 + 80 + 150 = 300문제에서 인접합 슬라임 2개를 합친 다고 했으므로, 아래와 같은 k가 반드시 존재합니다.
dp_{i,j}가 i 부터 j 까지 슬라임을 합칠 때, 최소비용으로 합치는 경우라고 정의합니다.
\begin{aligned}
1 \leq i < j \leq N \\
(i \leq k \: and \: k < j) \: or \: (i < k \: and \: k \leq j) \\
dp_{i,j} = dp_{i,k} + dp_{k,j} \\
\end{aligned}dp_{i,j}로 위에서 정의한 것은 뒤에서 다시 사용하도록 하구요,
dp_1 부터 시작해 보겠습니다.
\begin{aligned}
dp_1 = a_1 \\
\end{aligned}dp_2 는
\begin{aligned}
dp_2 = a_1 + a_2 \\
\end{aligned}dp_3 는 부터는 아래와 같이 2가지 경우가 생기게 되고, 둘 중의 최소값을 선택해야 합니다.
\begin{aligned}
dp_3 = min((a_1 + a_2) + (a_1 + a_2) + a_3 ,\; a_1 + (a_2 + a_3) + (a_2 + a_3)) \\
\end{aligned}위의 식을 dp_3 에서 dp_{1,3}으로 고처 써 보면,
\begin{aligned}
dp_{1,3} = min((a_1 + a_2) + (a_1 + a_2) + a_3 ,\; a_1 + (a_2 + a_3) + (a_2 + a_3)) \\
\end{aligned}a_1 + a_2 + a_3 이 양쪽에 모두 있으므로, 아래와 같이 고처 쓸 수 있습니다.
\begin{aligned}
dp_{1,3} = min((a_1 + a_2) ,\; (a_2 + a_3)) + (a_1+a_2+a_3) \\
dp_{1,3} = min((a_1 + a_2) ,\; (a_2 + a_3)) + \sum_{x=1}^3 a_x \\
\end{aligned}위의 식을 그대로, 1,2에서 적용해 보면,
\begin{aligned}
dp_{1,2} = min((a_1) ,\; (a_2)) + \sum_{x=1}^2 a_x \\
\end{aligned}위의 식을 그대로, 2,3에서 적용해 보면,
\begin{aligned}
dp_{2,3} = min((a_2) ,\; (a_3)) + \sum_{x=2}^3 a_x \\
\end{aligned}아래 Sample Input 에 대해서, 위의 점화식을 적용해 보면 아래 그림과 같이 오답이 나오게 됩니다.
3 1 2 3
위의 그림에서, 빨간색이 오답, 파란색이 정답인대, 위에서 새운 점화식 대로 하면, 빨간색의 오답이 계산됩니다. 여기서 좀더 고민해 볼 부분은, 아래와 같습니다. dp_{1,2}의 정답 3은 사실 오답 4에서 -1 하면 정답이 됩니다. 만약에 dp_1_2가 올바르게 계산되어서, 3이 되었다면, dp_{1,3}은 우리가 새운 점화식 대로, 정답을 계산할 수 있습니다.
위에서 dp_1 부터 dp_3 까지 오면, dp_1을 a_1으로 정의한 것 때문에, 사실 dp_1,1 이 a_1이 되었는대, dp_{1,1} 과 dp_{2,2}, dp_{3,3}을 0 으로 두면, dp_{1,2}를 계산할 때, a_1을 더하지 않게 됨으로, 정답을 계산하게 됩니다.
즉, 위의 그림에 보라색 X 표 처럼, dp_{i,j}일 때, i == j 이면, a_i가 아닌 0으로 두고, 위의 점화식대로 계산하면, dp_{1,N}에 정답을 계산할 수 있습니다.
위의 점화식을 고처쓰면,
\begin{aligned}
dp_{1,3} = min(dp_{1,2} ,\; dp_{2,3}) + \sum_{x=1}^3 a_x \\
\end{aligned}1,3을 i,j를 사용해서, 일반화 시킬 수 있습니다.
\begin{aligned}
dp_{i,j} = min(dp_{i,j-1} ,\; dp_{i+1,j}) + \sum_{x=i}^j a_x \\
\end{aligned}위의 점화식에 보면, a_x 의 특정 구간 부분집합을 자주 계산하게 되는 것을 알 수 있습니다. 왜냐하면, 문제 풀이를 시작할 때, k 의 존재에 대해서 설명했었구요, 이에 따라서, 아래와 같은 i, k구간 k+1, j 구간의 합을 자주 계산하게 됩니다. 이부분을 좀더 빠르게 계산하기 위해서 prefix sum 알고리즘을 사용해서, 보다 빠르게 계산할 수 있습니다. prefix sum은 여기 참고
마지막으로 dp_{1_4} 를 설명하고, 이번 문제 풀이를 마무리 하겠습니다. 글의 앞부분에서 k가 존재하는 범위에 대해서 설명한 것 과 같이 dp_{1_4} 는 아래와 같이 3가지 경우중에 최소값을 선택해야 합니다.
\begin{aligned}
dp_{1,4} = min(dp_{1,1}+dp_{2,4} \:, dp_{1,2}+dp_{3,4} \:, dp_{1,3}+dp_{4,4}) + \sum_{x=1}^4 a_x \\
\end{aligned}수식으로 표현하면, j-i 값이 커짐에 다라서, 위와 같이 min 에 들어가야할 항의 개수가 많아 지면서, 점점 길어짐니다.
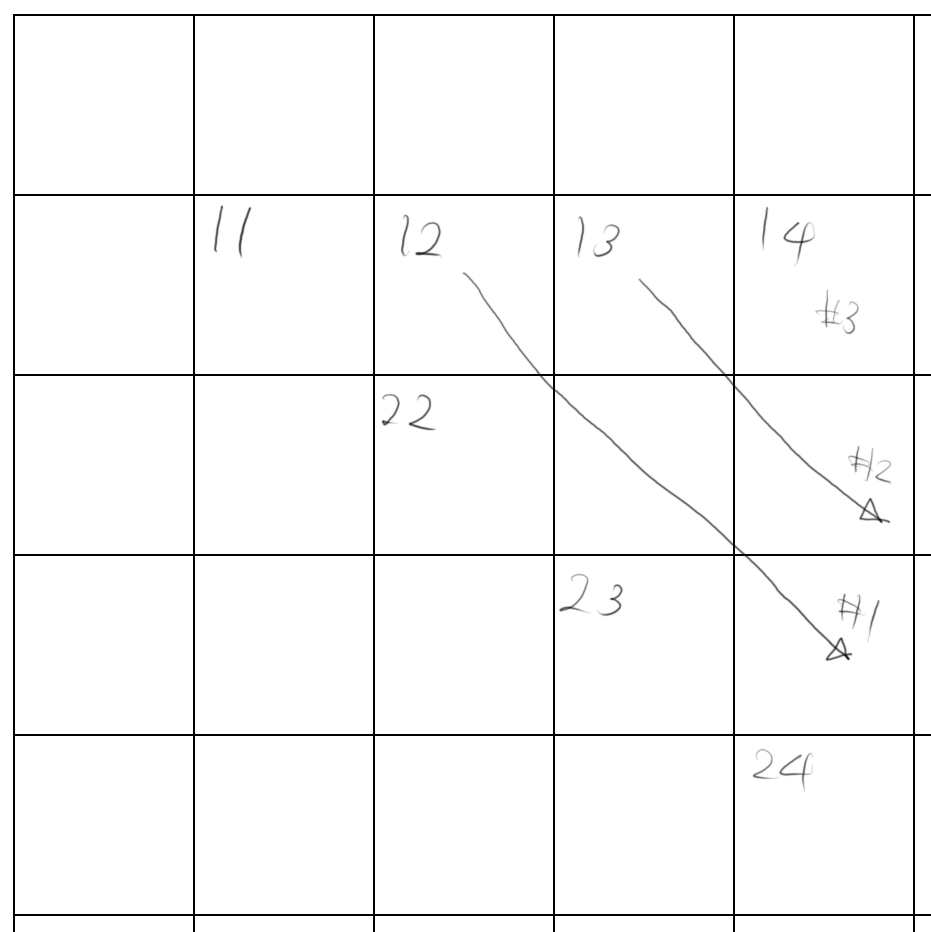
자바 코드로 표현하면 좀더 간결하게 표현할 수 있습니다.for(int k=i; k<j; ++k) { dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k+1][j] + (prefixSum[j] - prefixSum[i-1])); }마지막으로 dp_{i_j}를 계산하는 방향은 아래와 그림과 같습니다. #1~#3 순서로 계산합니다.
import java.io.DataInputStream; import java.io.FileInputStream; import java.io.IOException; import java.util.Scanner; /** * N - Slimes / atcoder.jp * 문제링크 : https://atcoder.jp/contests/dp/tasks/dp_n * 문제해설 : https://jinpyo.kim/EducationalDP-solution * Submission : https://atcoder.jp/contests/dp/submissions/9653540 */ public class Main { public static void main(String[] args) throws IOException { // Scanner sc = new Scanner(System.in); Reader sc = new Reader(); int N = sc.nextInt(); long[] as = new long[N+1]; long[][] dp = new long[N+1][N+1]; long[] prefixSum = new long[N+1]; for(int i=1; i<=N; ++i) { as[i] = sc.nextLong(); prefixSum[i] = prefixSum[i-1] + as[i]; } for(int ij_d=1; ij_d<=N; ++ij_d) { for(int i=1; i+ij_d<=N; ++i) { int j = i+ij_d; dp[i][j] = Long.MAX_VALUE; for(int k=i; k<j; ++k) { dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k+1][j] + (prefixSum[j] - prefixSum[i-1])); } } } System.out.println(dp[1][N]); } // https://www.geeksforgeeks.org/fast-io-in-java-in-competitive-programming/ static class Reader { final private int BUFFER_SIZE = 1 << 16; private DataInputStream din; private byte[] buffer; private int bufferPointer, bytesRead; public Reader() { din = new DataInputStream(System.in); buffer = new byte[BUFFER_SIZE]; bufferPointer = bytesRead = 0; } public Reader(String file_name) throws IOException { din = new DataInputStream(new FileInputStream(file_name)); buffer = new byte[BUFFER_SIZE]; bufferPointer = bytesRead = 0; } public String nextLine() throws IOException { byte[] buf = new byte[64]; // line length int cnt = 0, c; while ((c = read()) != -1) { if (c == '\n') break; buf[cnt++] = (byte) c; } return new String(buf, 0, cnt); } public int nextInt() throws IOException { int ret = 0; byte c = read(); while (c <= ' ') c = read(); boolean neg = (c == '-'); if (neg) c = read(); do { ret = ret * 10 + c - '0'; } while ((c = read()) >= '0' && c <= '9'); if (neg) return -ret; return ret; } public long nextLong() throws IOException { long ret = 0; byte c = read(); while (c <= ' ') c = read(); boolean neg = (c == '-'); if (neg) c = read(); do { ret = ret * 10 + c - '0'; } while ((c = read()) >= '0' && c <= '9'); if (neg) return -ret; return ret; } public double nextDouble() throws IOException { double ret = 0, div = 1; byte c = read(); while (c <= ' ') c = read(); boolean neg = (c == '-'); if (neg) c = read(); do { ret = ret * 10 + c - '0'; } while ((c = read()) >= '0' && c <= '9'); if (c == '.') { while ((c = read()) >= '0' && c <= '9') { ret += (c - '0') / (div *= 10); } } if (neg) return -ret; return ret; } private void fillBuffer() throws IOException { bytesRead = din.read(buffer, bufferPointer = 0, BUFFER_SIZE); if (bytesRead == -1) buffer[0] = -1; } private byte read() throws IOException { if (bufferPointer == bytesRead) fillBuffer(); return buffer[bufferPointer++]; } public void close() throws IOException { if (din == null) return; din.close(); } } }728x90'atcoder.jp' 카테고리의 다른 글
L - Deque / atcoder.jp (0) 2020.01.18 K - Stones / atcoder.jp (0) 2020.01.16 I - Coins / atcoder.jp (0) 2020.01.13 H - Grid 1 / atcoder.jp (0) 2020.01.01 G - Longest Path / atcoder.jp (0) 2020.01.01